AVL树
本质就是平衡二叉查找树
特点:
增加和删除几点后通过树形旋转重新打到平衡 左子树根右子树之间的高度差不能超过1
红黑树
主要特征是每个节点增加一个属性表示节点的颜色 可以是红色也可以是黑色 他追求的并不是绝对的平衡 而是保证从根节点到叶子节点的最长路径不超过最短路径的2倍 他的最坏运行时间复杂度是logn下面我会提供这个时间复杂度的证明
红黑树有五个约束条件 虽然我都不知道这些条件为什么是这样 有什么用 但是还是觉得这就是人家定下来的规则吧 肯定有人家的道理(达到防止红黑树野蛮往一个方向生长的效果)
- 节点只能是红色或者黑色
- 根节点必须是黑色
- 所有NIL结点都是黑色的 NIL就是叶子结点下挂着的两个虚节点
- 一条路径上不能出现相邻的两个红色节点
- 在任何递归子树内 根节点到叶子结点的所有路径上包含相同的黑色结点
旋转
无论是AVL树还是红黑书 旋转都是很常见的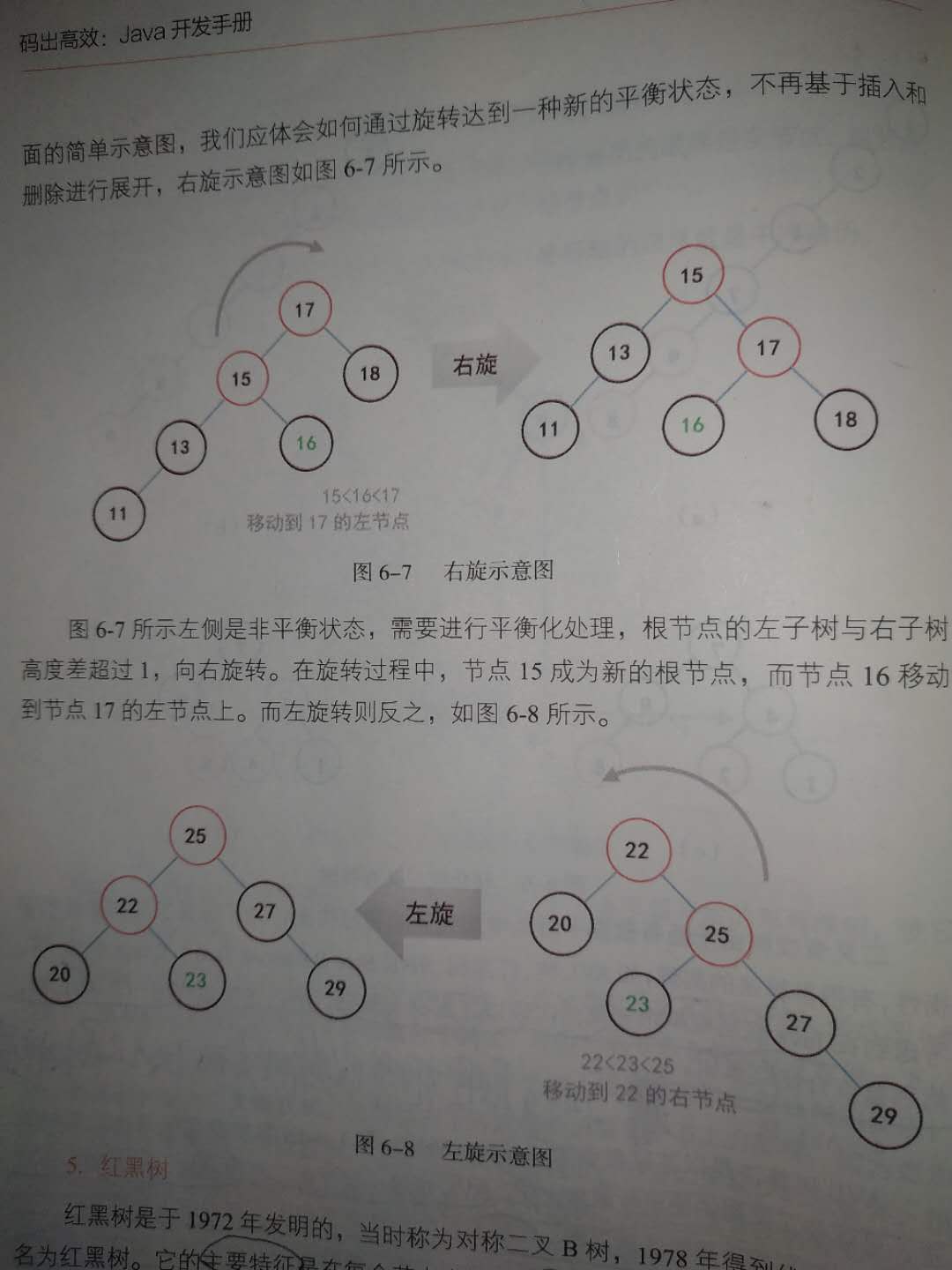
比较
因为AVL树追求的是绝对的平衡 红黑树追求的是大致上的平衡 所以相同的情况下红黑树很有可能比AVL树更高 那么查找的次数更多
另一方面 AVL树在回溯的时间成本上最差可能为logn 而红黑树每次回溯的部署步长为2 成本更低
所以
- AVL树更合适低频修改 大量查询
- 红黑树频繁的插入和删除
红黑树时间复杂度
我们知道红黑树插入和删除最差的时间复杂度都是logn 那么是怎样来的呢
首先由红黑书最后两个约束条件:
- 一条路径上不能出现相邻的两个红色结点
- 在任何递归子树内 根节点到叶子结点的所有路径上包含相同数目的黑色节点
由上面两个条件可以知道红黑树中的黑色节点都是分部均匀的 但是极端的情况下可以是整棵红黑树都是黑色节点
现在我们来认识一个新概念黑深度Black Depth 顾名思义就是当前节点到NIL节点途径上的黑色节点个数
那么对于根节点和上面两个约束条件 我们知道:
Black Depth >= height / 2
因为约束条件导致黑深度分布均匀 而且因为红红不相连 所以黑深度是大于等于半个深度的
我们假设红黑书的形状接近满二叉树的时候 假设有n个节点 高度为h 那么有:
2 ^ h - 1 = n
那么就有
h = log2(n + 1)
当一棵红黑树全是黑色节点的时候 那么根节点的黑深度就等于上面的h了 那么就有
log2(n + 1) >= height / 2
可以得到
height <= 2log2(n + 1)
我们知道红黑树的插入 是从根节点找到NIL的过程 时间复杂度就是
O(height) = O(2log2(n + 1)) = O(2log2(n + 1)) = O(2log2(2n)) = O(logn)
所以综上所述 红黑树在查找 插入 删除等 最坏时间复杂度是O(logn)
不知道上面的证明严谨不严谨 但是可以让我理解了 并且记忆深刻一点